本节主要讲的是动态规划,其面对的问题通常是无法一蹴而就,需要把复杂的问题分解成简单具体的小问题,然后通过求解简单问题,去推出复杂问题的最终解。
思想
大事化小,小事化了。把一个复杂的问题分阶段进行简化,逐步化简成简单的问题。
概念
1、动态规划 动态规划(Dynamic Programming)指的是解最优化问题的一种方法。
2、最优子结构性质 问题的最优解可以分解为若干子问题,且子问题的解也是最优的; 以上台阶为例,到第i层的最多走法,可以分解为第i-1层和第i-2层的走法之和,且第i-1层和第i-2层的走法也是最多的;
3、 无后效性 现阶段的决策不会影响未来的决策; 以上台阶为例,走到第i-2层的最多走法,不会因为增加第i-1层而改变;
思考过程
动态规划的思考过程可以总结为:大事化小,小事化了。 大事化小: 一个较大的问题,通过找到与子问题的重叠,把复杂的问题划分为多个小问题,也称为状态转移; 小事化了: 小问题的解决通常是通过初始化,直接计算结果得到;
具体的步骤
- 1、将大问题分解为子问题
- 2、确定状态表示
- 3、确定状态转移
- 4、考虑初始状态和边界情况
上台阶
有一个楼梯总共n个台阶,只能往上走,每次只能上1个、2个台阶,总共有多少种走法。
解决方案: 1、排列组合; 枚举2的个数,再枚举2具体放的位置; 计算复杂,容易遗漏。
2、动态规划; dp[n] 表示n个台阶的走法,那么有: dp[n]=dp[n-1]+dp[n-2];
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
// 有一个楼梯总共n个台阶,只能往上走,每次只能上1个、2个台阶,总共有多少种走法。
class GetClimbingWays {
func getClimbingWays(_ n: Int) -> Int {
if n < 1 {
return 0
}
if n == 1 {
return 1
}
if n == 2 {
return 2
}
var a = 1
var b = 2
var temp = 0
for _ in 3..<n {
temp = a + b
a = b
b = temp
}
return temp
}
}
斐波拉契数列
斐波拉契数列是这样一个数列:1, 1, 2, 3, 5, 8, … 除了第一个和第二个数字为1以外,其他数字都为之前两个数字之和。现在要求第100个数字是多少。
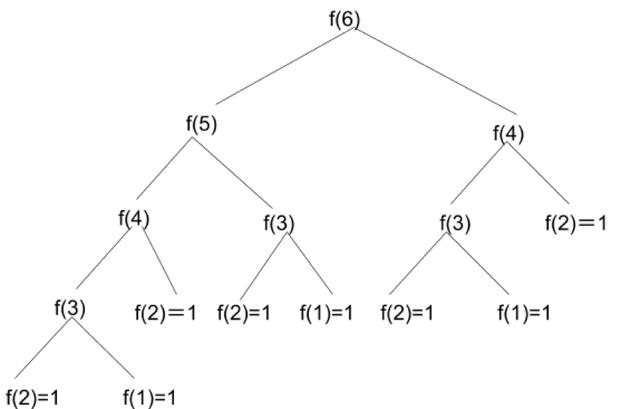
这道题目乍一看是一个数学题,那么要求第100个数字,很简单,一个个数字算下去就是了。假设F(n)表示第n个斐波拉契数列的数字,那么我们易得公式F(n) = F(n - 1) + F(n - 2),n >= 2,下面就是体力活。当然这道题转化成代码也不是很难,最粗暴的解法如下:
1
2
3
4
5
6
7
8
9
func Fib() -> Int {
var (prev, curr) = (0, 1)
for _ in 1 ..< 100 {
(curr, prev) = (curr + prev, curr)
}
return curr
}
用动态规划怎么写呢?首先要明白动态规划有以下几个专有名词:
- 初始状态,即此问题的最简单子问题的解。在斐波拉契数列里,最简单的问题是,一开始给定的第一个数和第二个数是几?自然我们可以得出是1
- 状态转移方程,即第n个问题的解和之前的 n - m 个问题解的关系。在这道题目里,我们已经有了状态转移方程F(n) = F(n - 1) + F(n - 2)
所以这题要求F(100),那我们只要知道F(99)和F(98)就行了;想知道F(99),我们只要知道F(98)和F(97)就行了;想要知道F(98),我们需要知道F(97)和F(96)。。。,以此类推,我们最后只要知道F(2)和F(1)的值,就可以推出F(100)。而F(2)和F(1)正是我们所谓的初始状态,即 F(2) = 1,F(1) =1。所以代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
func Fib(_ n: Int) -> Int {
// 定义初始状态
guard n > 0 else {
return 0
}
if n == 1 || n == 2 {
return 1
}
// 调用状态转移方程
return Fib(n - 1) + Fib(n - 2)
}
print(Fib(100))
这种递归的写法看起来简洁明了,但是上面写法有一个问题:我们要求F(100),那么要计算F(99)和F(98);要计算F(99),我们要计算F(98)和F(97)。。。大家已经发现到这一步,我们已经重复计算两次F(98)了。而之后的计算中还会有大量的重复,这使得这个解法的复杂度非常之高。解决方法就是,用一个数组,将计算过的值存起来,这样可以用空间上的牺牲来换取时间上的效率提高,代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
var nums = Array(repeating: 0, count: 100)
func Fib(_ n: Int) -> Int {
// 定义初始状态
guard n > 0 else {
return 0
}
if n == 1 || n == 2 {
return 1
}
// 如果已经计算过,直接调用,无需重复计算
if nums[n - 1] != 0 {
return nums[n - 1]
}
// 将计算后的值存入数组
nums[n - 1] = Fib(n - 1) + Fib(n - 2)
return nums[n - 1]
}
动态转移虽然看上去十分高大上,但是它也存在两个致命缺点:
- 栈溢出:每一次递归,程序都会将当前的计算压入栈中。随着递归深度的加深,栈的高度也越来越高,直到超过计算机分配给当前进程的内存容量,程序就会崩溃。
- 数据溢出:因为动态规划是一种由简至繁的过程,其中积蓄的数据很有可能超过系统当前数据类型的最大值,导致崩溃。
而这两个bug,我们上面这道求解斐波拉契数列第100个数的题目就都遇到了。
- 首先,递归的次数很多,我们要从F(100) = F(99) + F(98) ,一直推理到F(3) = F(2) + F(1),这样很容易造成栈溢出。
- 其次,F(100)应该是一个很大的数。实际上F(40)就已经突破一亿,F(100)一定会造成整型数据溢出。
当然,这两个bug也有相应的解决方法。对付栈溢出,我们可以把递归写成循环的形式(所有的递归都可改写成循环);对付数据溢出,我们可以在程序每次计算中,加入数据溢出的检测,适时终止计算,抛出异常。
数塔
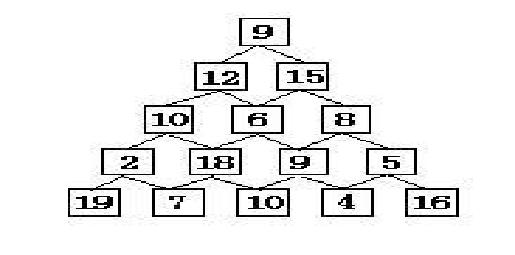
有如图所示的数塔,要求从顶层走到底层,若每一步只能走到相邻的结点,则经过的结点的数字之和最大是多少?
解决思路:
1、大事化小。
要到达第i层,先要到达第i-1层。并且第i层的第j个节点,只能由i-1层的第j个和第j-1个节点到达。
我们用dp[i][j]表示,走到第i层第j个位置的数字最大和。
那么有
1
dp[i][j]=max(dp[i-1][j], dp[i-1][j-1]) + a[i][j];
2、小事化了。第1层的第1个节点,初始值为dp[1][1]=a[1][1]。(a[x][y]表示第x层,第y个的值)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Triangle {
func minimumTotal(_ triangle: [[Int]]) -> Int {
guard !triangle.isEmpty else {
return 0
}
var mins = triangle.last!
for i in (0..<triangle.count - 1).reversed() {
let rows = triangle[i]
for j in (0..<rows.count) {
mins[j] = rows[j] + min(mins[j], mins[j + 1])
}
}
return mins[0]
}
}